Self-similar Groups and Fractals

Pink Fractal — Picture created by Kevin Dooley.

In this mathematics extension project, I will begin with a very brief introduction to self-similar groups, a quite new branch in pure mathematics. Then its connection with fractal geometry and their applications will be elaborated, followed by a set of worksheet on the topic of self-similarity and fractals. To finish this worksheet, you should be familiar with the topic of Series and Applications in Year 11 Mathematics syllabus.

Self-similar Groups

Murray Elder is a mathematician at the University of Technology, Sydney, whose research interests include geometric group theory, complexity theory and several other pure maths fields. In his paper A Short Introduction to Self-similar Groups (Elder, 2013), he introduced the concept of self-similar groups, a fascinating research area in geometric group theory. The following discussion is based on his paper and my interview with him on self-similar groups and other related topics like fractal geometry.

Self-similar is a widely used mathematical term, while self-similar groups are one branch analyzing the actions applied to an infinite rooted tree, T. A binary tree, T (see Figure 1.1), is composed of nodes (such as the root, 0, 1, 00, 01, …) and edges (the dashes joining two nodes). To briefly elaborate the idea of self-similar groups of T, we need to first define the meaning of an action (or “automorphism”) of T.
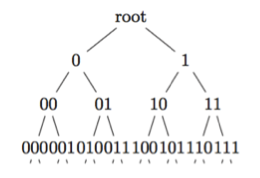
Fig1.1

(Figure 1.1. A binary tree T)

By convention, a star sign (*) drawn at a node of T means the following subtrees need to be exchanged: the left edge and its consecutive subtree would be moved to the right side and vice versa. Actions of the binary tree T can be defined with the star signs. We will then define three actions: a, b and e and construct a self-similar group with them.

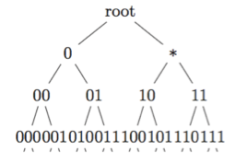
Action a: the star sign drawn at the root (see Figure 1.2) means the nodes “0” and “1” should be exchanged, and so are their consecutive subtrees.

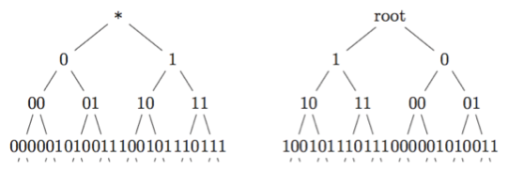Fig1.2 (Figure 1.2. The definition of a and the tree T after a)

Action b: the star was drawn at the node “1” (see Figure 1.3), which means the left subtree will be kept unchanged, but the subtrees on the right side will be exchanged.

Fig1.3 (Figure 1.3. The definition of b)

Action e: the binary tree T will remain unchanged after applying action e. This action can also be named as the identity, whose role is analogous to the zero in the addition operation and the number 1 in multiplication.

We can see that the action b refers to the actions a and e: its left subtree uses the identity e and its right subtree uses the action a. Similarly, the action a uses e: its left subtree refers to e’s right subtree and vice versa. Thus, we say the set {a, b, e} is self-referring or self-similar. And the group generated by the set {a, b, e} is a self-similar group. This group may seem totally abstract to you. But here is another intuitive and much more accessible definition of “self-similar”, that is, if we take a small piece of a self-similar object and zoom in, it will appear exactly the same as the whole object. By adopting this definition, we can have a look at some more exciting self-similar groups now. Using the Schreier graphs, an effective graphic device, we can depict the self-similar Basilica Group on the 4^th and 5^th levels (Figure 1.4, 1.5)(Elder, 2013).

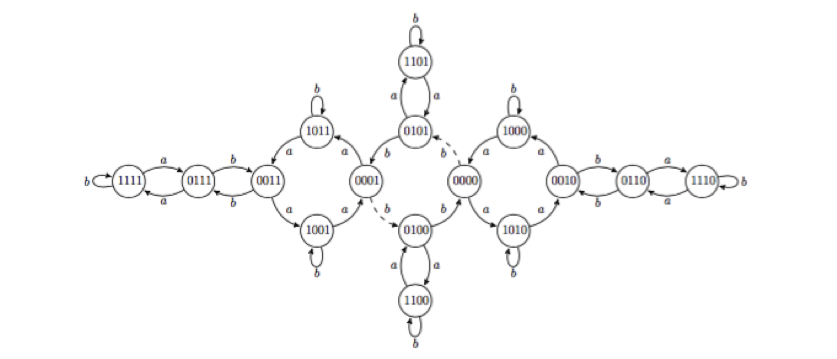Fig1.4 (Figure 1.4)

Fig1.5 (Figure 1.5)

Apparently, we cannot draw the whole picture of the group since there are infinite levels within. But we can imagine when the level goes on and on, the graph will keep repeating itself. And if we take just one piece of the whole graph, it will appear the same as the whole object.

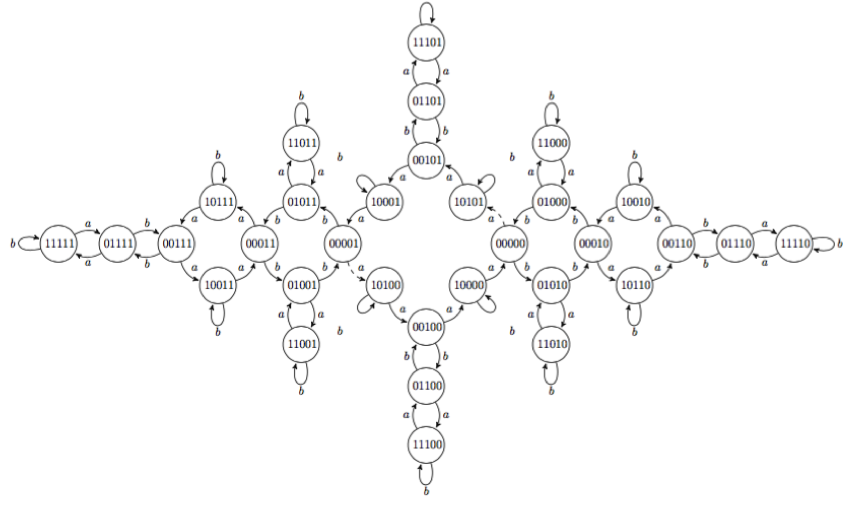
Here is another Schreier graph for the self-similar Hanoi Tower Group on the 4^th levels

Fig1.6 (Figure 1.6).

These graphs well demonstrated their properties of self-similarity. And when mathematicians seeing these graphs, they related them to another interesting geometric branch: the fractals (Nekrashevych & Teplyaev, 2008)!

Fractals

Fig2.1

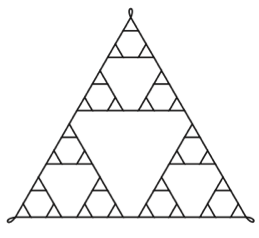
(Figure 2.1).

Figure 2.1 is a famous fractal shape, the Sierpinski triangle on the 4^th level. You can find it just coincides with the Schreier graph for Hanoi Tower Group (Figure 1.6)! How amazing is that! But what is a “fractal”?

A fractal is actually an object or quantity that displays self-similarity on all scales. The Sierpinski triangle is an example of fractal shapes, which can be created by iterating the processes in Figure 2.2 (“Fractal”, n.d.).

Figure2.2

(Figure 2.2, retrieved from http://mathworld.wolfram.com/Fractal.html)

The fractal shapes are beautiful and sometimes bizarre, while this geometric branch has enormous applications in the real world. Many shapes in nature are very similar to fractals, such as the ferns, cauliflowers, blood vessels, snowflakes, coastlines, river networks, even the structures of our lungs (Fractals, n.d.). These shapes may seem totally random to you, but with the understanding of fractal geometry, mathematicians can discover the basic patterns underlying these natural shapes and the rules by which these shapes are formed. In other words, mathematics enables us to understand these shapes deeper, thus applying our understandings in medicine, biology, geology and many other fields.

Additionally, just like the example of the Sierpinski triangle and the Hanoi Tower Group, mathematicians have also found a connection between the fractal shapes and the self-similar groups (Nekrashevych & Teplyaev, 2008). More than their visual similarity, there is a direct relation between these two branches, “which makes it possible to represent many well-known fractals as limit spaces of contracting self-similar groups, thus endowing them with additional algebraic structure.” (Nekrashevych & Teplyaev, 2008). Since fractals are more accessible than its homomorphism – the self-similar groups, we will focus on a fractal shape in the following worksheet: Von Koch Snowflake. It is a brilliant representation of the beauty and unique properties of fractal shapes. By exploring the construction and properties of the Koch Snowflake, we will have a taste of the topics of fractals and its property of self-similarity.

Worksheet on Self-similarity and Koch Snowflake

Solutions

Now, here is a bonus video, hope you wil enjoy it!